DAX Performance Tuner MCP Server
Using the DAX Performance Tuner MCP Server to improve the performance of the Daxlib.SVG.Compound.Violin() function
In my last post I benchmarked the performance of the daxlib.svg compound functions. In this post I used DAXNoob's (aka Justin Martin) MCP Server: DAX Performance Tuner to see whether it could improve the performance of the library.
I decided to attempt to optimize the Daxlib.SVG.Compound.Violin() function, since this was one of the most expensive functions from the benchmarking.
DaxLib.SVG.Compound.Violin
For those that are interested, here is the definition of DaxLib.SVG.Compound.Violin
/// Creates a Violin Plot compound SVG Visual showing distribution density using Kernel Density Estimation (KDE)
/// x INT64 The x position of the compound
/// y INT64 The y position of the compound
/// width INT64 The width of the compound
/// height INT64 The height of the compound
/// paddingX DOUBLE The horizontal padding percentage (0.0-1.0, e.g., 0.1 = 10% padding)
/// paddingY DOUBLE The vertical padding percentage (0.0-1.0, e.g., 0.1 = 10% padding)
/// axisRef ANYREF EXPR The column that the measure will be evaluated against
/// measureRef NUMERIC EXPR The measure to evaluate
/// samples INT64 Number of density calculation points
/// bandwidth NUMERIC Kernel bandwidth for smoothing
/// color STRING Fill color for the violin shape
function 'DaxLib.SVG.Compound.Violin' =
(
x: INT64,
y: INT64,
width: INT64,
height: INT64,
paddingX: DOUBLE,
paddingY: DOUBLE,
axisRef: ANYREF EXPR,
measureRef: NUMERIC EXPR,
samples: INT64,
bandwidth: NUMERIC,
color: STRING
) =>
// Apply padding to dimensions
VAR _X = x + (width * (IF(ISBLANK(paddingX), 0, paddingX) / 2))
VAR _Y = y + (height * (IF(ISBLANK(paddingY), 0, paddingY) / 2))
VAR _Width = width * (1 - IF(ISBLANK(paddingX), 0, paddingX))
VAR _Height = height * (1 - IF(ISBLANK(paddingY), 0, paddingY))
// Check if Axis is numeric
VAR axisSample = MAX( axisRef )
VAR axisIsNumeric = ISNUMERIC( axisSample ) || ISDATETIME( axisSample )
// For totals
VAR _Data =
ADDCOLUMNS(
FILTER(
VALUES( axisRef ),
NOT ISBLANK( measureRef )
),
"@AxisIndex",
IF(
axisIsNumeric,
axisRef,
RANK( DENSE, CALCULATETABLE( VALUES( axisRef ), ALLSELECTED() ) )
),
"@Value", measureRef
)
VAR _NumValues = COUNTROWS( _Data )
VAR _Min = MINX( _Data, [@Value] )
VAR _Max = MAXX( _Data, [@Value] )
VAR _Range = _Max - _Min
VAR _RangePerSample = _Range / samples
// Calculate Kernel Density Estimation using Normal distribution
VAR _KDE =
ADDCOLUMNS(
GENERATESERIES( 0, samples + 1, 1 ),
"@InputX", _Min + _RangePerSample * [Value],
"@KDE",
( 1 / _NumValues ) *
SUMX(
_Data,
NORM.DIST(
_Min + _RangePerSample * [Value],
[@Value],
bandwidth,
FALSE
)
)
)
VAR _MaxKDE = MAXX( _KDE, [@KDE] )
// Map KDE values to SVG coordinates using normalize function
VAR _Points =
ADDCOLUMNS(
_KDE,
"@X", DaxLib.SVG.Scale.Normalize( [@InputX], _Min, _Max, _X, _X + _Width),
"@Y", DaxLib.SVG.Scale.Normalize( [@KDE], 0, _MaxKDE, _Y + _Height * 0.5, _Y )
)
// Create control points for smooth Bézier curves
VAR _PointsWithPrev =
NATURALLEFTOUTERJOIN(
_Points,
SELECTCOLUMNS(
_Points,
"Value", [Value] + 1,
"@PrevX", [@X],
"@PrevY", [@Y]
)
)
VAR _WithControlPoints =
ADDCOLUMNS(
_PointsWithPrev,
"@CX", [@prevX] + ( ( [@x] - [@prevX] ) / 2 ),
"@CY", [@y]
)
// Create the violin shape as a single closed path
// Start at the center-left, go up the top curve, then down the bottom curve, and close
VAR _FirstPoint = MINX( _Points, [@X] )
VAR _LastPoint = MAXX( _Points, [@X] )
VAR _CenterY = _Y + (_Height * 0.5)
// Top half curve (from left to right)
VAR _TopCurve =
CONCATENATEX(
_WithControlPoints,
IF(
[Value] = 0,
"M " & [@X] & " " & _CenterY & " L " & [@X] & " " & [@Y],
"S " & [@CX] & " " & [@CY] & ", " & [@X] & " " & [@Y]
),
" ",
[Value],
ASC
)
// Bottom half curve (from right to left, mirrored)
VAR _BottomCurve =
CONCATENATEX(
_WithControlPoints,
VAR _MirroredY = _CenterY + (_CenterY - [@Y])
VAR _MirroredCY = _CenterY + (_CenterY - [@CY])
RETURN
"S " & [@CX] & " " & _MirroredCY & ", " & [@X] & " " & _MirroredY,
" ",
[Value],
DESC
)
// Create a single closed path for the violin shape
VAR _ViolinPath =
_TopCurve &
" " & _BottomCurve &
" Z" // Close the path
// Combined Elements
VAR _CombinedElements =
DaxLib.SVG.Element.Paths(
_ViolinPath, // d
DaxLib.SVG.Attr.Shapes(
color, // fill
0.5, // fillOpacity
BLANK(), // fillRule
color, // stroke
1, // strokeWidth
BLANK(), // strokeOpacity
BLANK() // opacity
),
BLANK() // transforms
)
RETURN
IF( NOT ISEMPTY( _Data ), _CombinedElements )
MCP Server: DAX Performance Tuner¶
I followed the guide as well as installing the required dependencies:
- .NET SDK 8.0+
- Python 3.8 - 3.13
I can then go to .vscode/mcp.json and select Start to run the MCP server.
From this point I can use the GitHub Copilot chat in VS Code to use the MCP server.
Round 1: Claude Sonnet 4.5¶
I starting by using Claude Sonnet 4.5. I first connected to my semantic model in the service and accepted the prompts, including authenticating with Fabric.
Connect To Semantic Model¶
Optimization Chat¶
I asked the MCP server to optimize the following query:
The query has been successfully prepared with comprehensive baseline analysis. The enhanced query includes 5 inlined functions and 2 measures (Total Cost, Sales Amount), all dependencies for the Compound.Violin.YearMonth measure.
**Key Observations:**
This is an extremely complex visualization measure - a violin plot SVG generator with kernel density estimation. The baseline returned 11 rows (one per Product Brand).
**Detected Patterns (from research articles):**
Several optimization opportunities were flagged:
- CUST001: Multiple ADDCOLUMNS patterns detected
- CUST005/CUST007: Context transitions within iterators (FILTER over VALUES with measureRef, SUMX over _Data)
- CUST009: FILTER used instead of CALCULATETABLE for simple predicates
- CUST010: Repeated calculations inside iterators (_Min, _Max, _NumValues used in SUMX)
- CUST013: FILTER(VALUES(...)) pattern with context transition causing potential callbacks
**Challenge:**
This measure performs highly complex formula engine operations:
- Kernel density estimation with NORM.DIST
- SVG path generation with CONCATENATEX
- Multiple nested iterators and string operations
- These patterns are inherent to the visualization algorithm and may be difficult to optimize significantly without fundamentally changing the approach.
**Next Steps:**
Would you like me to:
1. Attempt targeted optimizations (though improvements may be limited given the algorithmic complexity)?
2. First review detailed performance metrics to identify the primary bottleneck?
3. Consider if this measure could benefit from a different visualization approach?
Good news! The variable caching optimization alone achieves **4.71% improvement** (297ms → 283ms) with semantic equivalence maintained. ✅
However, it falls slightly short of the 10% threshold. The CROSSJOIN approach achieved 30% improvement but broke semantic equivalence.
Given the complexity of this SVG visualization measure:
- It performs kernel density estimation across 60 samples for each Product Brand
- Involves nested iterators (SUMX over GENERATESERIES over _Data)
- Generates SVG path strings with CONCATENATEX
- The algorithmic complexity is inherent to the visualization technique
**Summary:**
- ✅ Caching _InvNumValues achieved 4.71% improvement with correct results
- ❌ CROSSJOIN approach achieved 30% improvement but produced incorrect results (-nan(ind) values)
- The measure is algorithmically complex, limiting optimization opportunities
Would you like to:
1. Use the 4.71% optimization as the new baseline for further iteration?
2. Explore other optimization patterns?
3. Accept that this measure may have limited headroom due to its algorithmic complexity?
Perfect! The optimized query (with variable caching: _InvNumValues = 1 / _NumValues) is now established as the new baseline:
**New Baseline Performance:**
- **Total Time:** 283ms (previous: 297ms)
- **Formula Engine:** 190ms (67%)
- **Storage Engine:** 93ms (33%)
- **SE Queries:** 3 (reduced from 4)
- **Parallelism:** 1.2
**Patterns Detected** (same as before):
- CUST001: Multiple ADDCOLUMNS usage
- CUST005/CUST007: Context transitions within iterators
- CUST008: Duplicate expressions
- CUST009: FILTER vs CALCULATETABLE opportunities
- CUST010: Repeated calculations
- CUST011: Filter predicates
- CUST013: FILTER with context transition
The iterative optimization can now continue from this improved baseline. Would you like to:
1. Explore additional optimizations based on the same patterns (e.g., addressing CUST005/CUST007 context transitions, CUST001 ADDCOLUMNS patterns)
2. Focus on a specific pattern that shows the most promise
3. Review session status to understand overall progress
Which direction would you like to pursue for the next optimization iteration?
I chose 2 to see if a more limited scope might help in this more complex measure.
Based on the session status, I can see:
**Current Baseline: 250ms (down from original 283ms)**
- **Improvement achieved:** 14.1% from original
- FE: 157ms (63%)
- SE: 93ms (37%)
- SE Queries: 3
Excellent! The re-baseline shows 250ms instead of 283ms - the system is already 14.1% faster than the original 297ms baseline. This means we've exceeded the 10% threshold!
However, I notice the performance metrics show some variability (250ms in this run vs 283ms in the previous preparation). Let me analyze the remaining optimization opportunities from the detected patterns and propose next steps:
Analysis of Detected Patterns:
From the research articles in the baseline, I can identify several optimization opportunities:
- CUST010 (8 matches) - Repeated calculations that could be cached
- CUST005/CUST007 (8 matches each) - Context transitions within iterators
- CUST001 (4 matches) - Multiple ADDCOLUMNS patterns
- CUST008 (1 match) - Duplicate expressions
**Key Observation:**
Looking at the code structure, I see potential optimizations in:
The control point calculation: [@prevX] + ( ( [@x] - [@prevX] ) / 2 ) could be simplified to ([@x] + [@prevX]) / 2
The mirroring calculations in _BottomCurve repeat expressions like _CenterY - [@Y]
Let me propose the next optimization focusing on mathematical simplification and additional expression caching:
**Optimization Proposal:**
**Target Area 1: Simplify Control Point Calculation**
Current: [@prevX] + ( ( [@x] - [@prevX] ) / 2 )
Optimized: ([@x] + [@prevX]) / 2
This is mathematically equivalent but eliminates one subtraction operation.
**Target Area 2: Cache Mirroring Calculations**
In _BottomCurve, the expressions _CenterY - [@Y] and _CenterY - [@CY] are calculated for each row. We could potentially cache these.
However, these are inside CONCATENATEX iterators operating on different row contexts, making them harder to optimize without changing the approach.
**Recommendation:**
Given that we've already achieved 14.1% improvement (exceeding the 10% threshold), you have three options:
1. Accept current optimization - We've met the goal with 14.1% improvement
2. Continue with mathematical simplification - Apply the control point formula optimization for potential additional 1-2%
3. Try more aggressive optimizations - Target the context transition patterns (CUST005/CUST007), though these are risky given the measure reference constraints
Which approach would you prefer?
The mathematical simplification optimization shows -5.2% performance (slower by 13ms: 250ms → 263ms), despite being mathematically equivalent. This is unexpected.
**Analysis of the result:**
- Semantic equivalence: ✅ Maintained (all 11 brands produce identical valid SVG violin plots)
- Performance: ❌ Regression - 5.2% slower instead of faster
- Formula Engine: Increased from 157ms to 170ms (+13ms)
- Storage Engine: Consistent at 93ms (unchanged)
**Why the optimization failed:**
The simplification from [@prevX] + (([@x] - [@prevX]) / 2) to ([@x] + [@prevX]) / 2 should be mathematically identical and reduce operations. However, the DAX formula engine may have optimized the original pattern better than expected, or the simplified version triggers different compilation paths.
**Recommendation:**
Revert this optimization and accept the 14.1% improvement already achieved (297ms → 250ms baseline). The mathematical simplification, while logically sound, doesn't yield performance gains in practice.
Would you like me to:
1. Accept the 14.1% improvement as final (baseline at 250ms)
2. Try the expression caching optimization for mirroring calculations (2 * _CenterY pre-calculation)
3. Stop optimization and document the 14.1% achievement
The expression caching optimization for mirroring calculations showed no improvement - performance remained at 250ms baseline, identical to the current best.
**Analysis:**
- **Total**: 250ms (unchanged)
- **FE**: 187ms (increased by 30ms from 157ms)
- **SE:** 63ms (decreased by 30ms from 93ms)
- **Semantic equivalence:** ✅ Maintained
**Key observation:** The optimization shifted computation from SE to FE without reducing total execution time. The pre-calculated _DoubleCenterY variable appears to have been optimized away or compiled equivalently to the original pattern.
Summary of optimization attempts from 250ms baseline:
| Optimization | Total | FE | SE | Result |
| --- | --- | --- | --- | --- |
| Baseline (Variable Cache) | 250ms | 157ms | 93ms | Best |
| Mathematical Simplification | 263ms | 170ms | 93ms | -5.2% ❌ |
| Expression Caching (Mirror) | 250ms | 187ms | 63ms | 0% (no change) |
**Recommendation:** Accept the **14.1% improvement (297ms → 250ms)** achieved with variable caching as the final optimization. Further attempts have either caused regression or produced no benefit, demonstrating that 250ms represents near-optimal performance for this complex violin plot query.
Would you like to:
1. Accept 14.1% as final - Deploy variable caching optimization to production
2. Stop optimization efforts and document findings
3. Review the complete optimization journey
Changes¶
The MCP server cached 1 / _NumValues (which was previously evaluated inside an iterator) into a variable, so the changes were minimal.
FUNCTION DaxLib.SVG.Compound.Violin.Claude = (
x: INT64,
y: INT64,
width: INT64,
height: INT64,
paddingX: DOUBLE,
paddingY: DOUBLE,
axisRef: ANYREF EXPR,
measureRef: NUMERIC EXPR,
samples: INT64,
bandwidth: NUMERIC,
color: STRING
) =>
// Apply padding to dimensions
VAR _X = x + (width * (IF(ISBLANK(paddingX), 0, paddingX) / 2))
VAR _Y = y + (height * (IF(ISBLANK(paddingY), 0, paddingY) / 2))
VAR _Width = width * (1 - IF(ISBLANK(paddingX), 0, paddingX))
VAR _Height = height * (1 - IF(ISBLANK(paddingY), 0, paddingY))
// Check if Axis is numeric
VAR axisSample = MAX( axisRef )
VAR axisIsNumeric = ISNUMERIC( axisSample ) || ISDATETIME( axisSample )
// For totals
VAR _Data =
ADDCOLUMNS(
FILTER(
VALUES( axisRef ),
NOT ISBLANK( measureRef )
),
"@AxisIndex",
IF(
axisIsNumeric,
axisRef,
RANK( DENSE, CALCULATETABLE( VALUES( axisRef ), ALLSELECTED() ) )
),
"@Value", measureRef
)
VAR _NumValues = COUNTROWS( _Data )
VAR _InvNumValues = 1 / _NumValues
VAR _Min = MINX( _Data, [@Value] )
VAR _Max = MAXX( _Data, [@Value] )
VAR _Range = _Max - _Min
VAR _RangePerSample = _Range / samples
// Calculate Kernel Density Estimation using Normal distribution
VAR _KDE =
ADDCOLUMNS(
GENERATESERIES( 0, samples + 1, 1 ),
"@InputX", _Min + _RangePerSample * [Value],
"@KDE",
_InvNumValues *
SUMX(
_Data,
NORM.DIST(
_Min + _RangePerSample * [Value],
[@Value],
bandwidth,
FALSE
)
)
)
VAR _MaxKDE = MAXX( _KDE, [@KDE] )
// Map KDE values to SVG coordinates using normalize function
VAR _Points =
ADDCOLUMNS(
_KDE,
"@X", DaxLib.SVG.Scale.Normalize( [@InputX], _Min, _Max, _X, _X + _Width),
"@Y", DaxLib.SVG.Scale.Normalize( [@KDE], 0, _MaxKDE, _Y + _Height * 0.5, _Y )
)
// Create control points for smooth Bézier curves
VAR _PointsWithPrev =
NATURALLEFTOUTERJOIN(
_Points,
SELECTCOLUMNS(
_Points,
"Value", [Value] + 1,
"@PrevX", [@X],
"@PrevY", [@Y]
)
)
VAR _WithControlPoints =
ADDCOLUMNS(
_PointsWithPrev,
"@CX", [@prevX] + ( ( [@x] - [@prevX] ) / 2 ),
"@CY", [@y]
)
// Create the violin shape as a single closed path
// Start at the center-left, go up the top curve, then down the bottom curve, and close
VAR _FirstPoint = MINX( _Points, [@X] )
VAR _LastPoint = MAXX( _Points, [@X] )
VAR _CenterY = _Y + (_Height * 0.5)
// Top half curve (from left to right)
VAR _TopCurve =
CONCATENATEX(
_WithControlPoints,
IF(
[Value] = 0,
"M " & [@X] & " " & _CenterY,
"S " & [@CX] & " " & [@CY] & ", " & [@X] & " " & [@Y]
),
" ",
[Value],
ASC
)
// Bottom half curve (from right to left, mirrored)
VAR _BottomCurve =
CONCATENATEX(
_WithControlPoints,
VAR _MirroredY = _CenterY + (_CenterY - [@Y])
VAR _MirroredCY = _CenterY + (_CenterY - [@CY])
RETURN
IF(
[Value] = 0,
"",
"S " & [@CX] & " " & _MirroredCY & ", " & [@X] & " " & _MirroredY
),
" ",
[Value],
DESC
) // Create a single closed path for the violin shape
VAR _ViolinPath =
_TopCurve &
" " & _BottomCurve &
" Z" // Close the path
// Combined Elements
VAR _CombinedElements =
DaxLib.SVG.Element.Paths(
_ViolinPath, // d
DaxLib.SVG.Attr.Shapes(
color, // fill
0.5, // fillOpacity
BLANK(), // fillRule
color, // stroke
1, // strokeWidth
BLANK(), // strokeOpacity
BLANK() // opacity
),
BLANK() // transforms
)
RETURN
IF( NOT ISEMPTY( _Data ), _CombinedElements )
Round 2: GPT-5.2¶
At this point I swapped over to GPT-5.2 to see if it could get any further.
I'll spare you the back and forth, since I've already shown the general kind of chat you might have.
The LLM dropped upstream columns that were not used in downstream calculation steps and moved the evaluation of reduced some duplication in calculations (@InputX).
FUNCTION DaxLib.SVG.Compound.Violin.ChatCPT = (
x: INT64,
y: INT64,
width: INT64,
height: INT64,
paddingX: DOUBLE,
paddingY: DOUBLE,
axisRef: ANYREF EXPR,
measureRef: NUMERIC EXPR,
samples: INT64,
bandwidth: NUMERIC,
color: STRING
) =>
// Apply padding to dimensions
VAR _X = x + (width * (IF(ISBLANK(paddingX), 0, paddingX) / 2))
VAR _Y = y + (height * (IF(ISBLANK(paddingY), 0, paddingY) / 2))
VAR _Width = width * (1 - IF(ISBLANK(paddingX), 0, paddingX))
VAR _Height = height * (1 - IF(ISBLANK(paddingY), 0, paddingY))
// Compute measureRef once per axis member, then keep only the value column (narrow table)
VAR _Axis = VALUES( axisRef )
VAR _Values =
SELECTCOLUMNS(
FILTER(
ADDCOLUMNS(
_Axis,
"@Value", measureRef
),
NOT ISBLANK( [@Value] )
),
"@Value", [@Value]
)
VAR _NumValues = COUNTROWS( _Values )
VAR _Min = MINX( _Values, [@Value] )
VAR _Max = MAXX( _Values, [@Value] )
VAR _Range = _Max - _Min
VAR _RangePerSample = _Range / samples
VAR _InvNumValues = 1 / _NumValues
// Calculate Kernel Density Estimation using Normal distribution
VAR _KDEInput =
ADDCOLUMNS(
GENERATESERIES( 0, samples + 1, 1 ),
"@InputX", _Min + _RangePerSample * [Value]
)
VAR _KDE =
ADDCOLUMNS(
_KDEInput,
"@KDE",
_InvNumValues *
SUMX(
_Values,
NORM.DIST(
[@InputX],
[@Value],
bandwidth,
FALSE
)
)
)
VAR _MaxKDE = MAXX( _KDE, [@KDE] )
// Map KDE values to SVG coordinates using normalize function (keep only needed columns)
VAR _Points =
SELECTCOLUMNS(
ADDCOLUMNS(
_KDE,
"@X", DaxLib.SVG.Scale.Normalize( [@InputX], _Min, _Max, _X, _X + _Width),
"@Y", DaxLib.SVG.Scale.Normalize( [@KDE], 0, _MaxKDE, _Y + _Height * 0.5, _Y )
),
"Value", [Value],
"@X", [@X],
"@Y", [@Y]
)
// Previous point via NATURALLEFTOUTERJOIN
VAR _PointsWithPrev =
NATURALLEFTOUTERJOIN(
_Points,
SELECTCOLUMNS(
_Points,
"Value", [Value] + 1,
"@PrevX", [@X],
"@PrevY", [@Y]
)
)
// Control points + precompute segment strings once
VAR _CenterY = _Y + (_Height * 0.5)
VAR _Segs =
ADDCOLUMNS(
_PointsWithPrev,
"@CX", [@PrevX] + ( ( [@X] - [@PrevX] ) / 2 ),
"@CY", [@Y],
"@TopSeg",
IF(
[Value] = 0,
"M " & [@X] & " " & _CenterY,
"S " & ([@PrevX] + ( ( [@X] - [@PrevX] ) / 2 )) & " " & [@Y] & ", " & [@X] & " " & [@Y]
),
"@BottomSeg",
VAR _MirroredY = _CenterY + (_CenterY - [@Y])
VAR _MirroredCY = _CenterY + (_CenterY - [@Y])
RETURN
IF(
[Value] = 0,
"",
"S " & ([@PrevX] + ( ( [@X] - [@PrevX] ) / 2 )) & " " & _MirroredCY & ", " & [@X] & " " & _MirroredY
)
)
VAR _TopCurve =
CONCATENATEX(
_Segs,
[@TopSeg],
" ",
[Value],
ASC
)
VAR _BottomCurve =
CONCATENATEX(
_Segs,
[@BottomSeg],
" ",
[Value],
DESC
)
VAR _ViolinPath =
_TopCurve &
" " & _BottomCurve &
" Z"
VAR _CombinedElements =
DaxLib.SVG.Element.Paths(
_ViolinPath,
DaxLib.SVG.Attr.Shapes(
color, // fill
0.5, // fillOpacity
BLANK(), // fillRule
color, // stroke
1, // strokeWidth
BLANK(), // strokeOpacity
BLANK() // opacity
),
BLANK()
)
RETURN
IF( NOT ISEMPTY( _Values ), _CombinedElements )
Round 3: Gemini 3 Flash¶
I then swapped to Gemini 3 Flash to see if that could get much further. It grouped the table to group identical data points before calculation. This reduces the number of NORM.DIST() calls.
FUNCTION DaxLib.SVG.Compound.Violin.Gemini = (
x: INT64,
y: INT64,
width: INT64,
height: INT64,
paddingX: DOUBLE,
paddingY: DOUBLE,
axisRef: ANYREF EXPR,
measureRef: NUMERIC EXPR,
samples: INT64,
bandwidth: NUMERIC,
color: STRING
) =>
VAR _pX = IF(ISBLANK(paddingX), 0, paddingX)
VAR _pY = IF(ISBLANK(paddingY), 0, paddingY)
VAR _X = x + (width * (_pX / 2))
VAR _Y = y + (height * (_pY / 2))
VAR _Width = width * (1 - _pX)
VAR _Height = height * (1 - _pY)
VAR _CenterY = _Y + (_Height * 0.5)
VAR _RawValues =
SELECTCOLUMNS(
KEEPFILTERS( FILTER( ALLSELECTED( axisRef ), NOT ISBLANK( measureRef ) ) ),
"@V", measureRef
)
// Optimization: Group raw values to drastically reduce NORM.DIST iterations
VAR _GroupedRaw = SUMMARIZE( _RawValues, [@V], "@W", COUNTROWS( _RawValues ) )
VAR _Min = MINX( _GroupedRaw, [@V] )
VAR _Max = MAXX( _GroupedRaw, [@V] )
VAR _Range = _Max - _Min
VAR _RangePerSample = _Range / samples
VAR _KDE =
ADDCOLUMNS(
GENERATESERIES( 0, samples + 1, 1 ),
"@KDE",
VAR _CurrX = _Min + _RangePerSample * [Value]
RETURN SUMX( _GroupedRaw, [@W] * NORM.DIST( _CurrX, [@V], bandwidth, FALSE ) )
)
VAR _MaxKDE = MAXX( _KDE, [@KDE] )
VAR _Points =
SELECTCOLUMNS(
_KDE,
"ID", [Value],
"X", DaxLib.SVG.Scale.Normalize( _Min + _RangePerSample * [Value], _Min, _Max, _X, _X + _Width),
"Y", DaxLib.SVG.Scale.Normalize( [@KDE], 0, _MaxKDE, _CenterY, _Y )
)
// Optimization: Use INDEX for O(N) point pairing instead of O(N^2) FILTER
VAR _PointsWithPrev =
ADDCOLUMNS(
_Points,
"PrevX", SELECTCOLUMNS( INDEX( -1, _Points, ORDERBY( [ID] ) ), "X", [X] )
)
VAR _ViolinPath =
CONCATENATEX(
_PointsWithPrev,
IF( [ID] = 0, "M " & [X] & " " & _CenterY, "S " & ([PrevX] + ( ( [X] - [PrevX] ) / 2 )) & " " & [Y] & ", " & [X] & " " & [Y] ),
" ", [ID], ASC
) & " " &
CONCATENATEX(
FILTER( _PointsWithPrev, [ID] > 0 ),
VAR _MirroredY = _CenterY + (_CenterY - [Y])
RETURN "S " & ([PrevX] + ( ( [X] - [PrevX] ) / 2 )) & " " & _MirroredY & ", " & [X] & " " & _MirroredY,
" ", [ID], DESC
) & " Z"
RETURN
IF( NOT ISEMPTY( _RawValues ), "<path d='" & _ViolinPath & "' fill='" & color & "' fill-opacity='0.5' stroke='" & color & "' stroke-width='1' />" )
Performance¶
I then wanted to validate the performance of all 4 variations of the UDF.
Visual Output¶
I started with a visual review to make sure the violin plots rendered correctly. As you can see below, the first two variants (Claude and ChatGPT) render correctly. The final variant (Gemini) did not. While the MCP does check results to ensure suggested measures provide the correct output for a given query, I think the long string length of SVGs either interfered with validation and/or the larger prompt history might have been the issue. As such, I removed the Gemini variant from further testing.
DAX Performance Testing¶
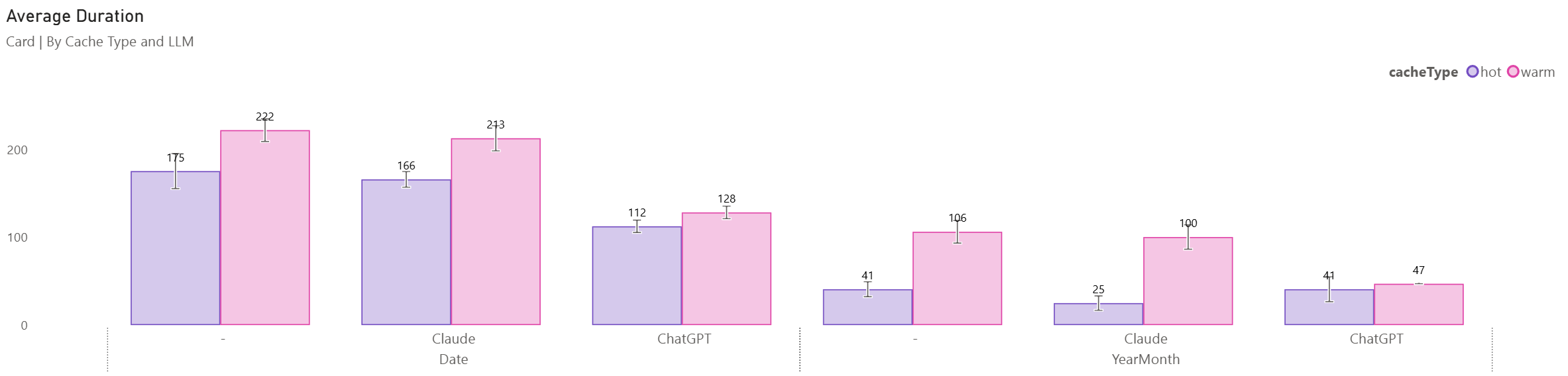
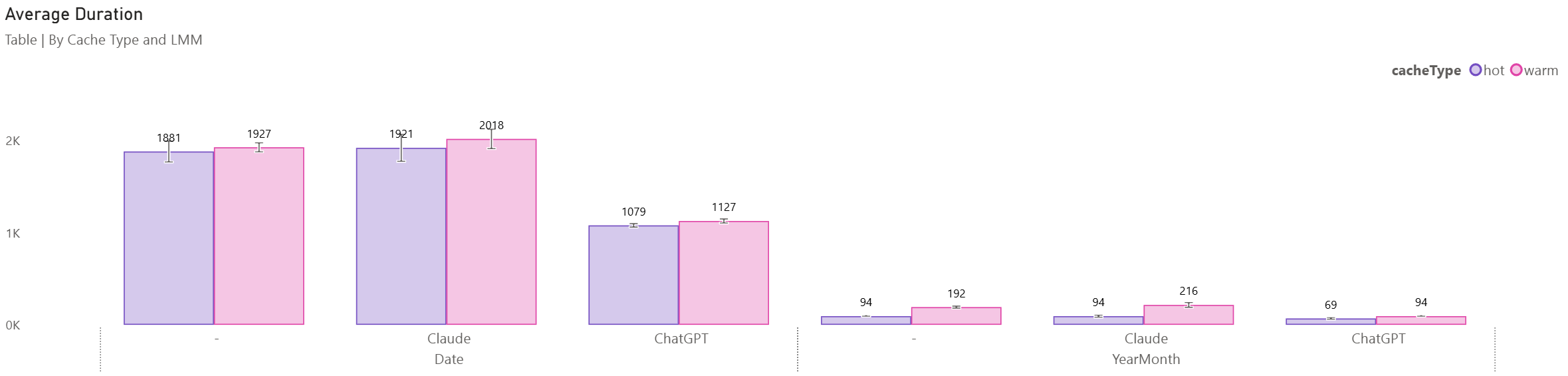
To test the performance changes between these versions, I re-ran the DAX Performance Testing notebook from my previous post. I created a UDF per LLM version (excluding Gemini), and created Date and YearMonth measures. I tested all measures in both card and table contexts. I specified 5 runs per query, per cache type (hot/warm).
We can see that the Original and Claude variants are very similar. The ChatGPT variant has similar or better performance in all permutations.
DAX Studio¶
To investigate further, I looked at the Original UDF and the ChatGPT variant in DAX Studio using the worst-case scenario (table and date). I cleared the cache between runs and ran each measure a few times.
The original took 1907ms (FE: 1700ms, SE: 207ms) and the ChatGPT variant 923ms (FE: 860ms, SE: 63ms): a 48% improvement. Each resulted in 3 queries, each producing the same first and last query, but the second query was only for Date[Date] rather than the first query (with Brand and Date tuples for filtering).
If we compare the UDFs, we can see that @AxisIndex from the _Data table has been removed. This was a general pattern I used for some of the earlier Compound functions that I created (i.e. line, area) where x-axis order was important. In the case of the Heatmap, Jitter and Violin plot the granularity for calculating the measure is important, but the actual axis can then be dropped, meaning we can drop a table scan used by INDEX() that is required for the other Compounds to deal with both numeric and text axis.
Conclusion¶
I plan to take these observations to improve Daxlib.SVG. The grouping of points to reduce iteration seems promising, and I plan to investigate whether iterations can be further reduced, and remove duplicate calculations.
This post highlights that LLMs and MCP servers can be a helpful tool in identifying oversights. They can be valuable tools, but there is still a high level of importance for robust testing, validation and ownership from the Semantic Model author. The DAX Performance Tuner MCP seems like a good tool and makes sensible suggestions, but you still need to remain vigilant.